Bitcoin – studium przypadku

Szanowni czytelnicy,
Zapewne nie wszyscy z Was znają Raport CERT Orange Polska, a być może także są wśród Was tacy, którzy nie wiedzą, czy zamieszczone w naszym corocznym wydawnictwie materiały wzbudzą ich zainteresowanie. Dlatego zdecydowaliśmy, że przez pewien czas raz w tygodniu będziemy publikować jeden materiał ekspercki, licząc, że część z Was przyciągnie on do przeczytania kolejnych. Wszystkie dotychczasowe edycje raportu są rzecz jasna dostępne za darmo na poświęconej im podstronie naszego serwisu. A póki co – zapraszamy do lektury artykułu autorstwa Adama Pichlaka: „Bitcoin – studium przypadku”.
Świat kryptowalut i technologii blockchain rozwija się w bardzo szybkim tempie. Bitcoin, który powstał jako pierwszy cieszy się największą popularnością. Z tego też względu uwaga cyberprzestępców w dużej mierze jest skierowana właśnie na niego.
W tym artykule przyjrzymy się bezpieczeństwu bitcoina i przyjrzymy się dwóm metodom jakimi posłużyli się cyberprzestępcy, aby ukraść cyfrowe monety (skupiając się na zasadzie działania sieci, nie podmiotów używających bitcoiny – takich jak giełdy itp.).
Aby zrozumieć działanie powstawania adresów w bitcoinie warto przypomnieć, jak działa tworzenie klucza publicznego z wykorzystaniem krzywych eliptycznych. Poniżej przestawiona została taka krzywa (wraz z naniesionymi punktami):
y² = x³ + 7
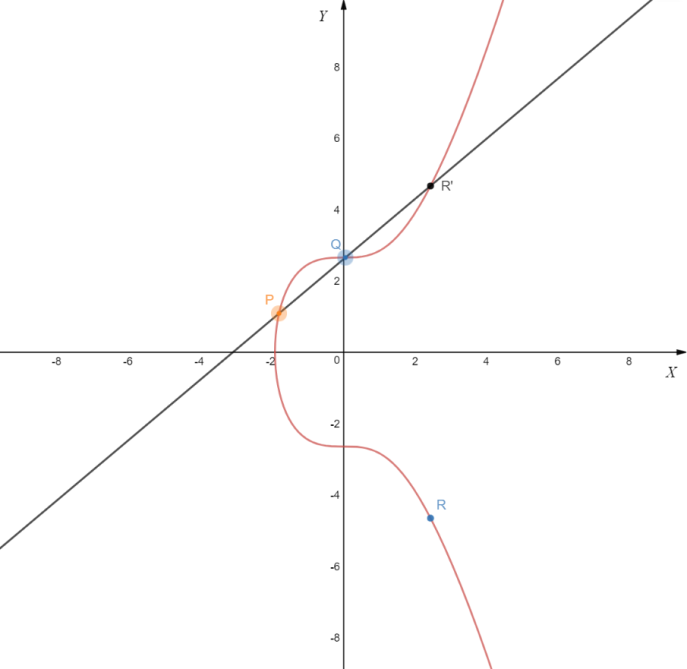
Przy obliczaniu klucza publicznego stosuje się dwa działania – dodawanie punktu i jego podwajanie. Aby dodać punkt P i Q należy przeprowadzić przez nie prostą, a punkt przecięcia jej z krzywą (poza tymi dwoma punktami) to punkt R’, który po rzutowaniu względem osi X daje punkt R.
Podwojenie punktu (np. początkowego G) polega na przeprowadzeniu stycznej w tym punkcie, a wspólny punkt tej stycznej i krzywej reprezentuje punkt 2G’, którego rzutowanie względem osi X daje punkt 2G.
Klucz prywatny jest wygenerowaną losową dużą liczbą (256 bitową), którą należy przemnożyć przez punkt początkowy G używany przez bitcoina – wynik działania to klucz publiczny, czyli współrzędne X i Y.
Klucz ten można także reprezentować wyłącznie za pomocą współrzędnej X (klucz publiczny skompresowany) – współrzędną Y można wówczas wyliczyć.
Dla przykładu, złamiemy zasadę tworzenia klucza prywatnego jako dużej losowej liczby – załóżmy ze jest to liczba 3. Na podstawie jej wyznaczmy klucz publiczny:
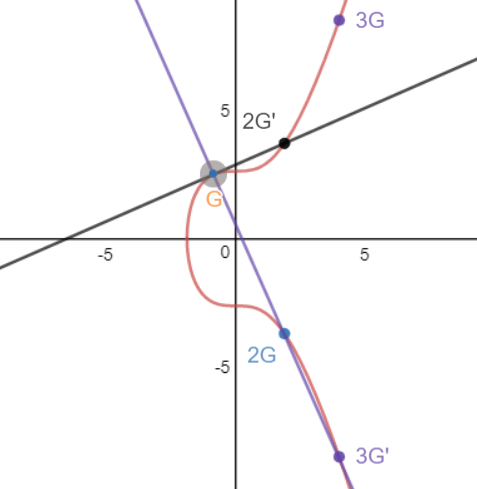
W dużym skrócie tak wygląda proces tworzenia klucza publicznego z użyciem równania krzywej eliptycznej w zakresie liczb rzeczywistych. W przypadku krzywej używanej przez bitcoina krzywą tą oblicza się w skończonym ciele, które reprezentuje dużą liczbę pierwszą: p = 2²⁵⁶ -2³²-2⁹-2⁸-2⁷-2⁶-2⁴-1, zatem wynik każdej kalkulacji musi zawierać się w tym przedziale, reprezentacja punktów będzie wyglądać inaczej – będą to losowo rozłożone punkty symetryczne względem osi X, a równanie będzie miało postać:
y² mod p = x³ + 7 mod p
W przypadku dużych liczb jest niezwykle trudno odzyskać klucz prywatny znając wyłącznie klucz publiczny. Aktualnie jedyną metodą jest próba przeszukania całego zakresu, która wymaga dużego nakładu mocy obliczeniowej i czasu.
Krzywe eliptycznie nie są wykorzystywane na potrzeby szyfrowania czegokolwiek w blockchainie, a po to by udowodnić „sieci”, że emisja transakcji jest rzeczywiście rozpoczęta przez właściciela portfela – poprzez podpis cyfrowy. Portfel to nic innego jak klucz prywatny z którego otrzymywany jest klucz publiczny, a z niego powstaje adres (a raczej para adresów – skompresowany i nieskompresowany – pomijamy tutaj adresy P2SH i segwit). Poniżej ten proces przedstawiony jest bardziej obrazowo:
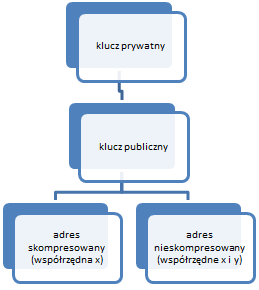
Proces tworzenia adresu skompresowanego i nieskompresowanego (różnica polega wyłącznie na 1 punkcie):
- Sha256 (02 + X) lub Sha256(04 + X + Y)
- Ripemd160(1.)
- 00 + 2.
- Sha256 (3.)
- Sha256 (4.)
- 3. + 4 pierwsze bajty 5.
- Base58 (6.)
Przykładowo, klucz prywatny będący haszem SHA256 słowa „secure” daje współrzędne X i Y
X: 33fef0a65b8d3dc5941d31e0a40ee4de32b59204ff37ec601750796f59dafb53
Y: 069997cd8badd15f862626c5a8d8859dbeed5b65da43bf9968469f99d372c46c
a jego adresy to:
nieskompresowany: 1CvTyRmJZ19gYUK4bUdmPX843oAmN3TZLF
skompresowany: 1AjJJHqa1sEvPWyMee6XCarxAgpRBpHmdG
Brainwallet
W portfelu deterministycznym (wprowadzonym w BIP-32), klucze powstają na podstawie klucza głównego (ziarna). Dokument BIP-39 definiuje tworzenie takiego ziarna i jego reprezentację jako wzorca – zestawu wyrazów mnemonicznych. Portfel ten można łatwiej zapamiętać, jest bardziej uporządkowany niż portfel losowy, a przede wszystkim odtworzenie ziarna pozwala na przywrócenie wszystkich kluczy. W przypadku ostatniej generacji portfeli deterministycznych entropia jest zbliżona do kluczy prywatnych stworzonych losowo. W celu stworzenia bezpiecznego portfela generowane jest ziarno, które reprezentuje 12 (i więcej) losowych słów spośród 2048 dostępnych (zdefiniowanych w BIP-39), później już może posłużyć do tworzenia jednego bądź wielu portfeli.
Brainwallet to wersja mechanizmu podobnego do portfela deterministycznego, która działa prosto: na podstawie danych wpisanych przez użytkownika, następuje stworzenie haszu SHA256 i zastosowanie go jako klucza prywatnego portfela – kolejne portfele mogły być tworzone na podstawie dodawania kolejno liczb do takiego hasła np.: secure1, secure2 itd. Wiązało się to ze znacznym obniżeniem bezpieczeństwa. Po pierwsze z powodu możliwości stworzenia portfela na podstawie krótkiego i niezłożonego hasła, po drugie z powodu tego, że jego twórcą człowiek, co może wiązać się z zastosowaniem powszechnie używanych słów. Próba ataku brute force klucza prywatnego jako skrót SHA256 hasła może doprowadzić do przejęcia środków na danym adresie. Ciekawe efekty uzyskamy stosując jako klucz prywatny kilkukrotne haszowanie takich haseł lub wykorzystanie innego algorytmu. Ilość portfeli, na które kiedykolwiek dokonano transakcji można liczyć w tysiącach.
Przykłady takich portfeli znajdują się poniżej:
Adres | Razem otrzymane | Aktualny stan |
14NWDXkQwcGN1Pd9fboL8npVynD5SfyJAE | 501.06510751 BTC | 0 |
158zPR3H2yo87CZ8kLksXhx3irJMMnCFAN | 30.28147684 BTC | 0 |
1CLq46YiBtXy7N3nCbKYm4hsJm4Z3Gyqvg | 7.33 BTC | 0 |
Niebezpieczne podpisy
Transakcja to proces przesunięcia pewnych środków z jednego adresu na inny. Transakcje zapisywane są trwale w łańcuchu bloków i każdy może podejrzeć ich szczegóły. Aby ją wygenerować i aby taka transakcja została zaakceptowana przez sieć, emitujący ją jako pierwszy, musi udowodnić, że jest właścicielem portfela, z którego przesyłane są środki. Używany jest w tym celu podpis cyfrowy. Podpisywanymi danymi są tutaj hasze wejść czyli wyjścia innych transakcji kierowane na ten adres.
Wzór na podpis:
S = k⁻¹*(m+R*d) mod n
Gdzie:
- S – podpis
- k – tymczasowy klucz prywatny
- m – hasz wejścia
- R – tymczasowy klucz publiczny
- d – klucz prywatny (adresu z którego emitowana jest transakcja)
- n – duża liczba pierwsza używana przez bitcoina
W podpisie dołączane są wartości S i R, sieć weryfikuje podpis przeliczając odpowiednio hasze wejść i tych dwóch wartości – jeśli wynik jest równy R wówczas transakcja jest prawidłowo podpisana i zaakceptowana.
Wartość k powinna być losowa i nie powtarzać się, jeśli tak nie jest, wówczas dwa podpisy jednego adresu, w których zastosowana jest ta sama wartość k pozwolą na wyciągnięcie klucza prywatnego poprzez rozwiązanie równania z dwoma niewiadomymi – k i d. Zakładając, że posiadamy wartości S₁, S₂, m₁, m₂ i R jesteśmy w stanie wyznaczyć równanie:
d = (S₂*m₁-S₁*m₂) * (R*(S₁-S₂))⁻¹ mod n
Choć transakcje tego typu zdarzały się w przeszłości i doprowadzało to do utraty środków, a błędy w podpisach są znane od lat, również w 2018 roku zostały one wygenerowane i pozwalały na odzyskanie kluczy prywatnych do trzech adresów. W 2018 roku dokonano nieznacznych wpłat na 7 adresów, których transakcje pozwoliły na wyliczenie klucza z poprzednich lat.
Z pewnością wysłanie środków na adres, którego klucz prywatny można z łatwością wyliczyć, zakończy się utratą ich w ciągu kilku minut.
Poniżej przykład w pythonie dla adresu 1CvTyRmJZ19gYUK4bUdmPX843oAmN3TZLF (jest to wyżej wymieniony adres, którego klucz prywatny jest skrótem SHA256 słowa „secure”, dane są przykładowe):
>>> import ECC >>> r = 0xc0eb253af8f097edb495e7406d22b0d141b4b80b689d378ed00d611fe8e915ae >>> m₁ = 0xee70560dd3e23bc28305804f9bdccd4fe5c11c6a35fbc609284403c9e55b981f >>> m₂ = 0x5898271f5a5528ee905880c2b841ab04c614e1ffd5c906392401bcb6ed2b414a >>> s₁ = 0xbac63ae591bf35e0c02b17215f7eb37452eef70c46428dca2f4c94dcff19e538 >>> s₂ = 0x2cfd1a89214ff6b9f8134875c917071b21e348acb303c5826cf128cc734d6675 >>> n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141 >>> private = (s₁ * m₂ – s₂ * m₁) * pow(r * (s₂ – s₁), n-2, n) % n >>> #sprawdzenie >>> P = ECC.ec.calc(private) >>> print ECC.BitAddress().getAddr(P.X, P.Y) 1CvTyRmJZ19gYUK4bUdmPX843oAmN3TZLF |
Takie błędy zdarzają się przede wszystkim z powodu nieprawidłowej implementacji podpisu np. poprzez generowanie liczb losowych z ziarnem, które może się powtórzyć. Aktualnie w najnowszych portfelach podpis generowany jest za pomocą deterministyczno-losowego mechanizmu, który generuje losową liczbę na podstawie danych z transakcji, dzięki czemu zawsze zmienna ta będzie różna.
Podsumowanie
Bitcoin to względnie nowa technologia, która stale jest udoskonalana. Przy korzystaniu z jej dobrodziejstw trzeba mieć zawsze na uwadze korzystanie z najnowszych wersji oprogramowania, ponieważ błędna implementacja może prowadzić do przejęcia portfela. Również tworząc system oparty na blockchainie trzeba zwrócić uwagę na bezpieczną implementacja kluczowych dla bezpieczeństwa mechanizmów. Przedstawione zostały tylko niektóre ze znanych podatności, na szczęście mają one aktualnie minimalną skalę, ale w dalszym ciągu są regularnie monitorowane przez przestępców.
Adam Pichlak


